最短路算法

最短路算法，见名知意，就是用于求出图中从某个顶点到另一个顶点最短距离的算法。最短路算法的应用极其广泛。本文将会以求解最短路为中心，围绕着展开叙述一些常见的最短路算法的原理和应用。

根据最短路算法，我们大致地可以将算法分为两大类：

1. 单源最短路径 Single Source Shortest Path：用于快速计算从某一个特定顶点出发到达任意一个点的距离。
2. 多源最短路径 Multiple Source Shortest Path：用于快速计算任意两点之间的最短路径。

本文将会介绍的算法和各算法的特点如下：

1. 深度优先搜索 Depth First Search：单源最短路径算法，可以求解从任意一点开始到另一点的最短路径，但该算法极其耗时。
2. 广度优先搜索 Breadth First Search：单源最短路径算法，仅用于求解无权图。
3. 迪克斯特拉算法 Dijkstra Algorithm：单源最短路径算法，是广度优先搜索算法的加强版。Dijkstra 算法不能处理带有负权边的情况，更不能处理带有负权回路的图。
4. 贝尔曼福特算法 Bellman-Ford Algorithm：单源最短路径算法，可以用于处理又负权边的情况。对其进行队列优化后就变成了我们熟知的 SPFA 算法。
5. 弗洛伊德算法 Floyd Algorithm：多源最短路径算法，基于动态规划思想，能够一次性求出图中任意两点之间的最短路径，但该算法的时间复杂度非常高，达到惊人的 $O(N^3)$。弗洛伊德算法能处理带有负权边的情况，但不能处理带有负权回路的图。

为了方便阅读，本文提供的所有代码均会使用 vector 实现的邻接表来存图。

场景引入

在下图中，有 $7$ 条不同的边，每一条路径上方都标记了一个数值 $T_i$，代表通过该条路径所需要的时间。Macw 想知道从 $1$ 号顶点到 $5$​ 号顶点所需要花费的最短时间。

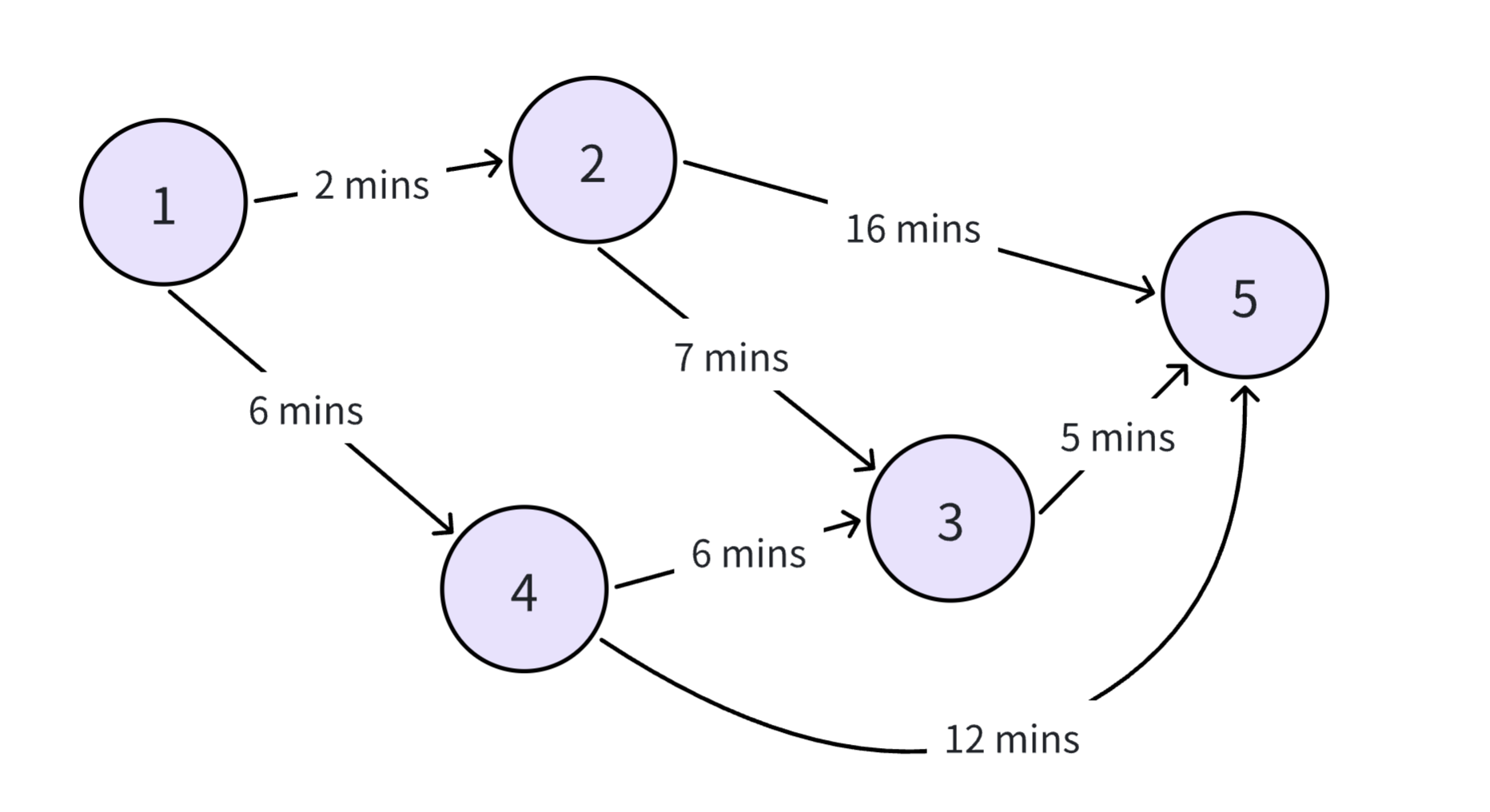
不难看出，Macw 所需要花费的最短时间是 $14$ 分钟，一条可行的方案是从 $1$ 号顶点出发，途径 $2$，$3$ 号顶点到达顶点 $5$。虽然人脑可以很快的看出来，但是在庞大的数据量下，人的脑力就显得极其渺小。那对于计算机来说，我们如何能找到一条从 $1$ 号节点到 $5$ 号节点的路径呢？不妨让计算机暴力枚举出所有的可行路径和每条路径分别的耗时，取最小的那一条路径就可以了。深度优先搜索算法是一个选择。