SPFA 算法
SPFA 算法 Shortest Path Faster Algorithm
SPFA (Shortest Path Faster Algorithm) 算法是 Bellman-Ford 算法的改进版本,专门用于加速单源最短路径的计算。该算法通过队列机制减少了不必要的松弛操作,从而提高了代码的运行效率。SPFA算法在实践中表现出优异的性能,特别是在稀疏图中。
SPFA 算法利用一个队列来存储需要松弛的顶点,并且每个顶点在队列中最多出现一次。通过这种机制,SPFA 算法避免了对所有边进行多余的松弛操作,从而提高了效率。
但 SPFA 算法也有缺陷,在一些特殊的情况下,可能会出现卡死的情况(有一句古话:关于 SPFA,它死了)。在最坏的情况下,SPFA 的复杂度高达 (就是普通 Bellman-Ford)算法的运行效率。但该算法在大多数情况下表现优异,通常情况该算法的平均时间复杂度在 附近,其中 是图中顶点的数量, 是图中边的数量。
SPFA 算法具体的实现流程如下:
- 初始化:
-
创建一个数组,用于记录从源点开始到任意一点的距离。同时设定源节点的距离为 ,其他所有节点的距离为 。
-
初始化一个队列(不需要是优先队列,普通队列即可)。将源点加入到队列之中。
-
初始化一个数组用来记录某个顶点是否在队列之中。在程序开始时,源点应该被标记为已经入队。
- 松弛操作:
- 对于每一条边 ,和这条边的权重 ,如果可以使得 ,则将 更新为 。其中, 表示编号为 节点的距离。
- 如果成功进行了松弛操作,且顶点 不在队列之中,那么将顶点 加入到队列之中。
- 重复执行:
- 重复第二部的操作,直到队列为空。
- PS:如果某个点加入了队列 次,则说明该图存在负环,应该立结束程序。
以下是使用 SPFA 算法对例题的模拟过程:
首先初始化距离数组,将源点的距离设置为 ,将除源点以外的所有点的距离设置为 。正无穷大表示到达该点的最短距离还未知。同时,将源点加入到队列之中,并将源点标记为已加入队列。
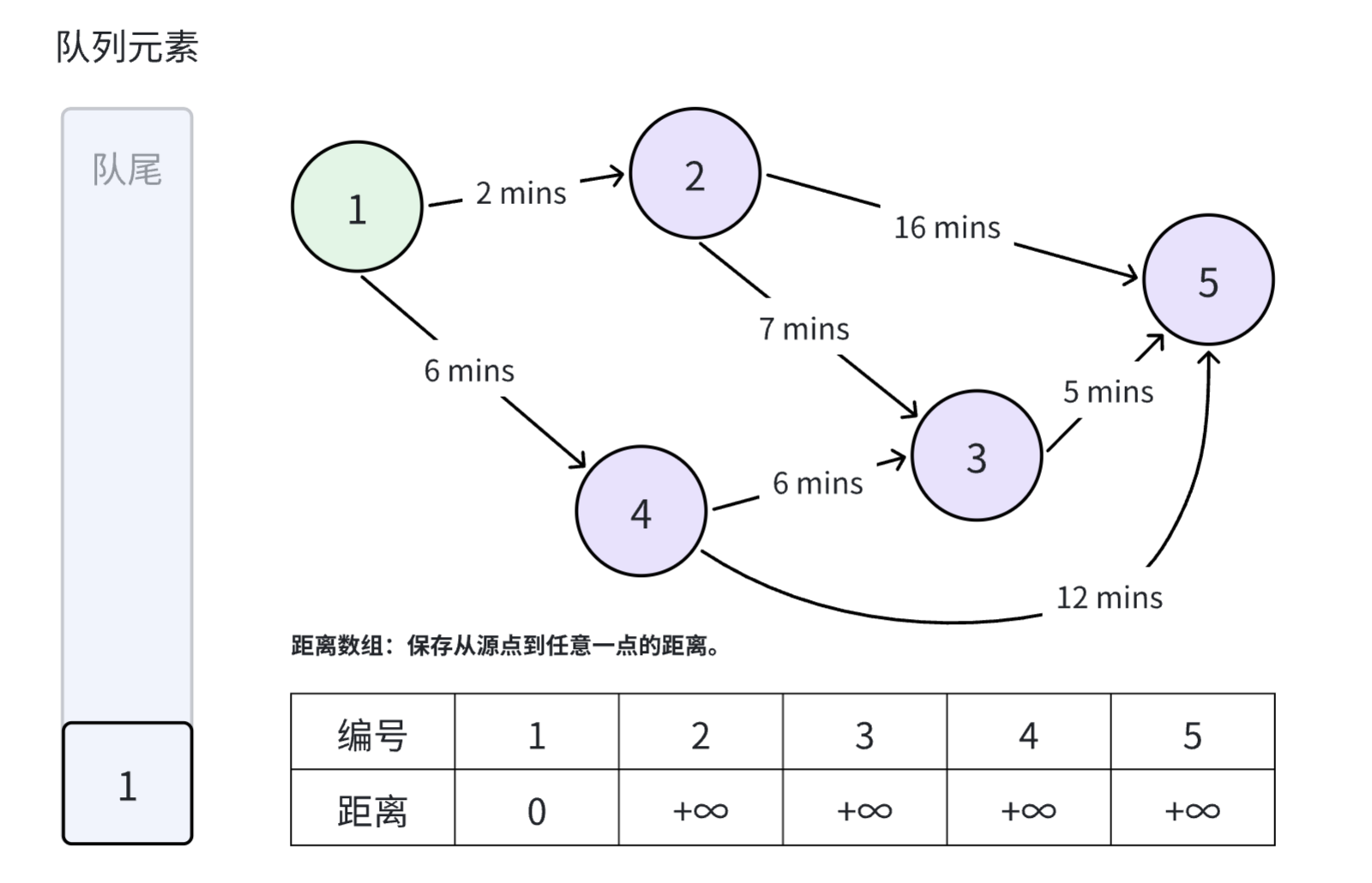
选择队首元素(在当前情况就是 ��号节点),松弛与 号节点相邻的两条边。从 号节点出发,到 号节点和 号节点的距离都比正无穷大要小,因此更新这两个节点的距离。与此同时,由于 号节点和 号节都不在队列中,因此将这两个节点加入到队列。
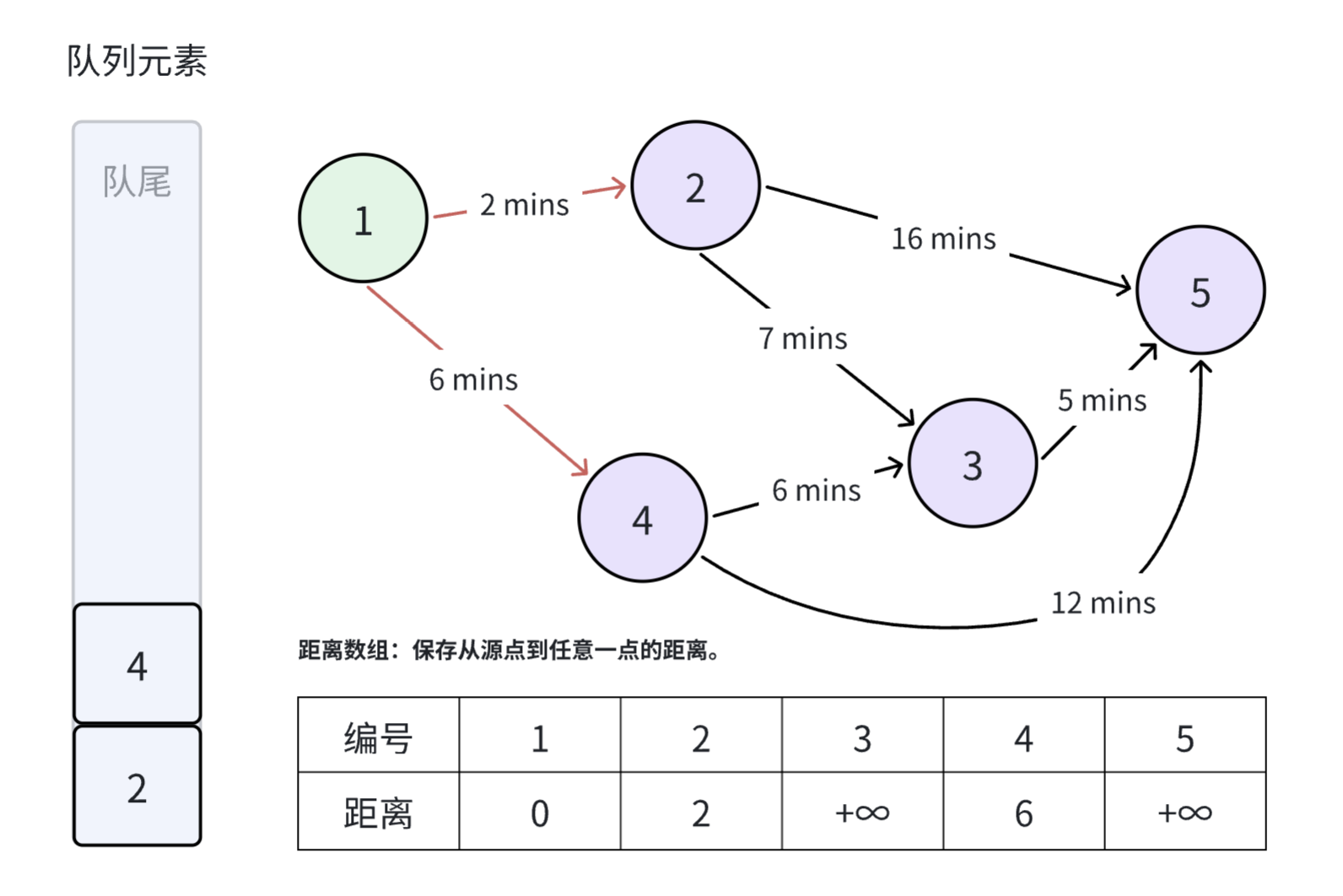
弹出位于队首的 号元素,选择位于队首的 号元素,松弛与 号节点相邻的两条边。从 号节点出发,到 号节点和 号节点的距离都比正无穷大要小,因此更新这两个节点的距离。与此同时,由于 号节点和 号节都不在队列中,因此将这两个节点加入到队列。
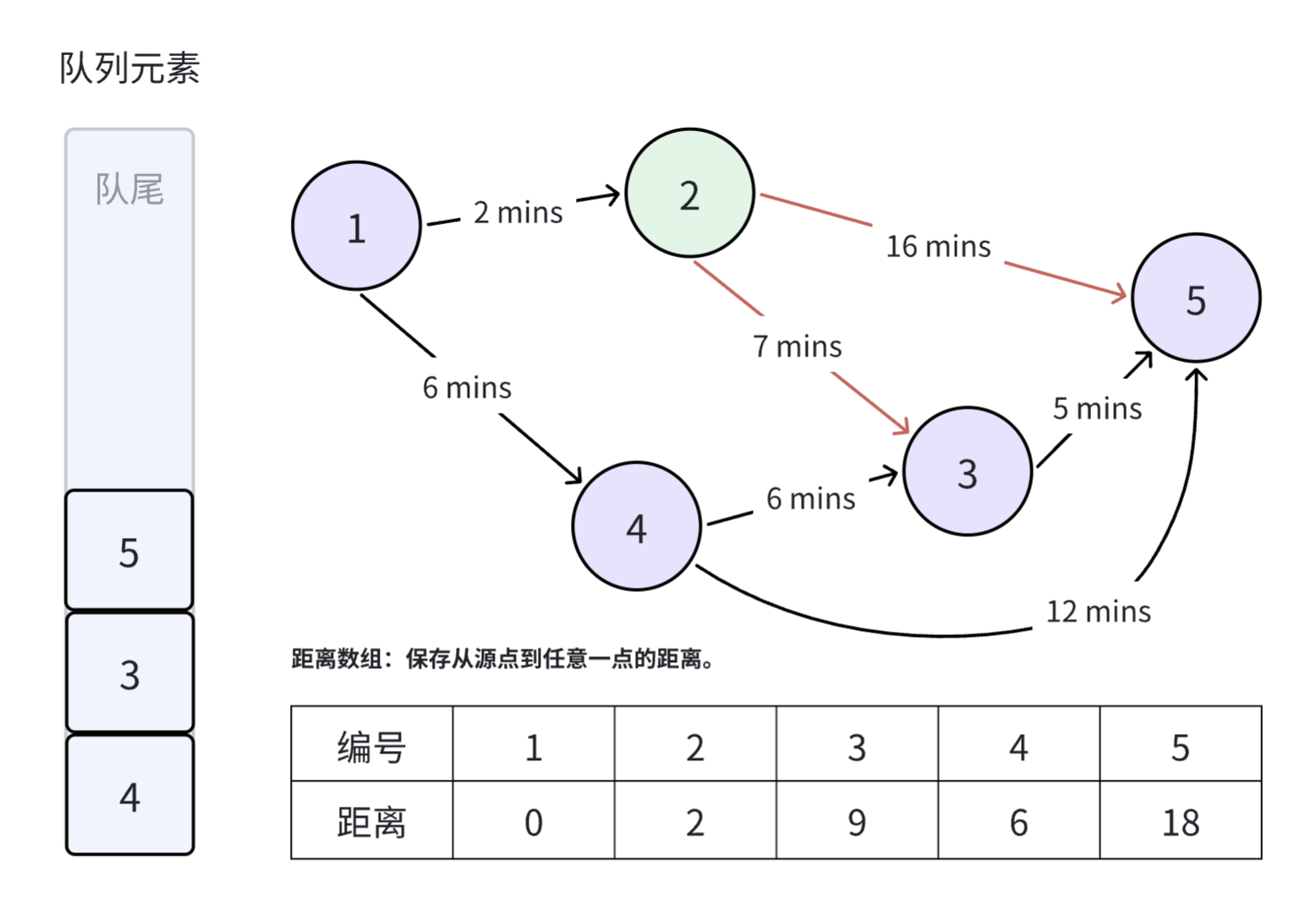
弹出位于队首的 号元素,选择位于队首的 号元素,松弛与 号节点相邻的两条边。从 号节点出发,到 号节点��和 号节点的距离都比原本要远,因此不更新任何节点,也不将任何节点加入到队列当中。
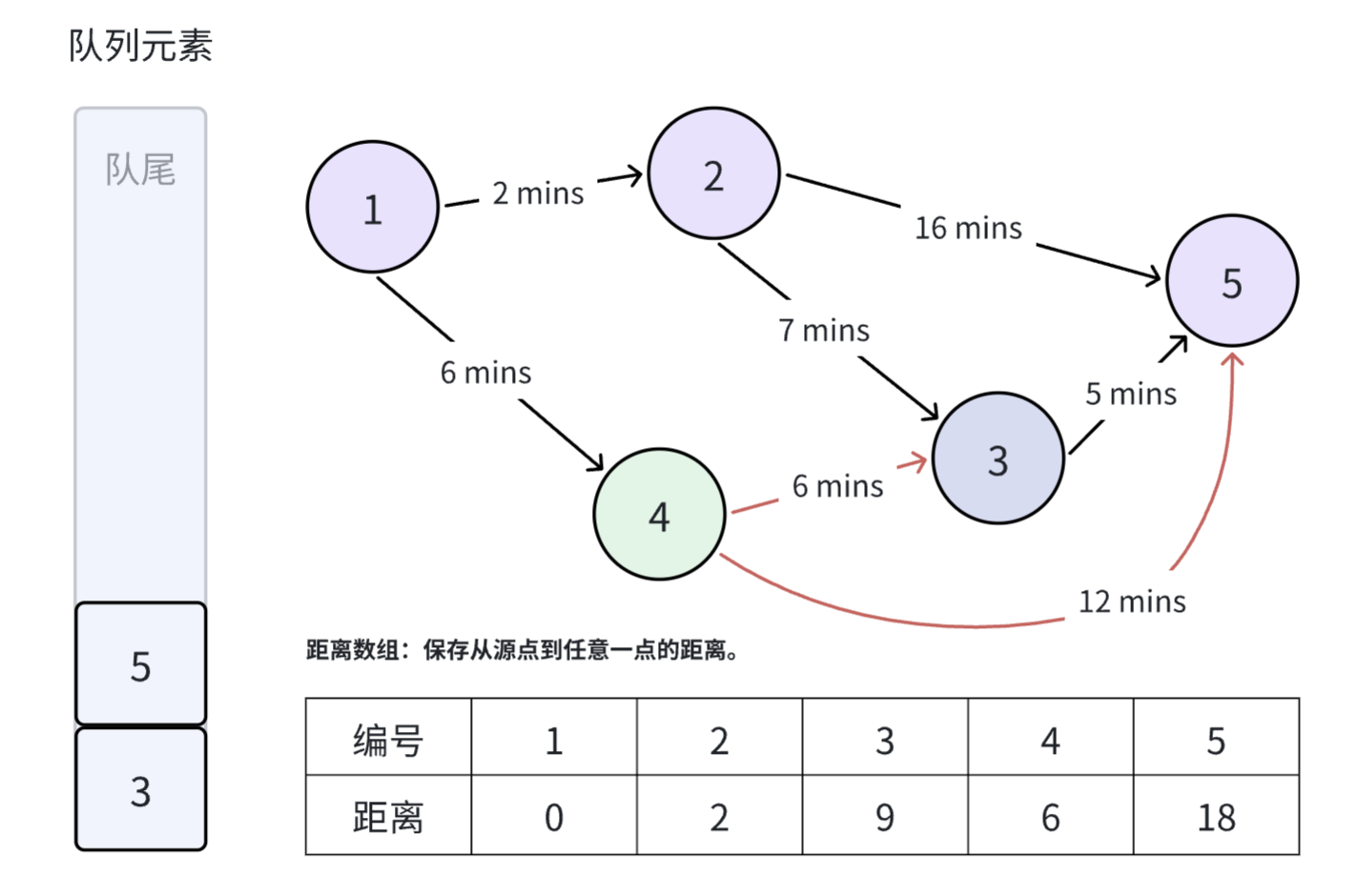
弹出位于队首的 号元素,选择位于队首的 号元素,松弛与 号节点相邻的两条边。从 号节点出发,到 号节点的距离为 ,比原本的 要更优,因此更新 号节点。但由于 号节点已经被加入到了队列之中,因此不再重复加入。
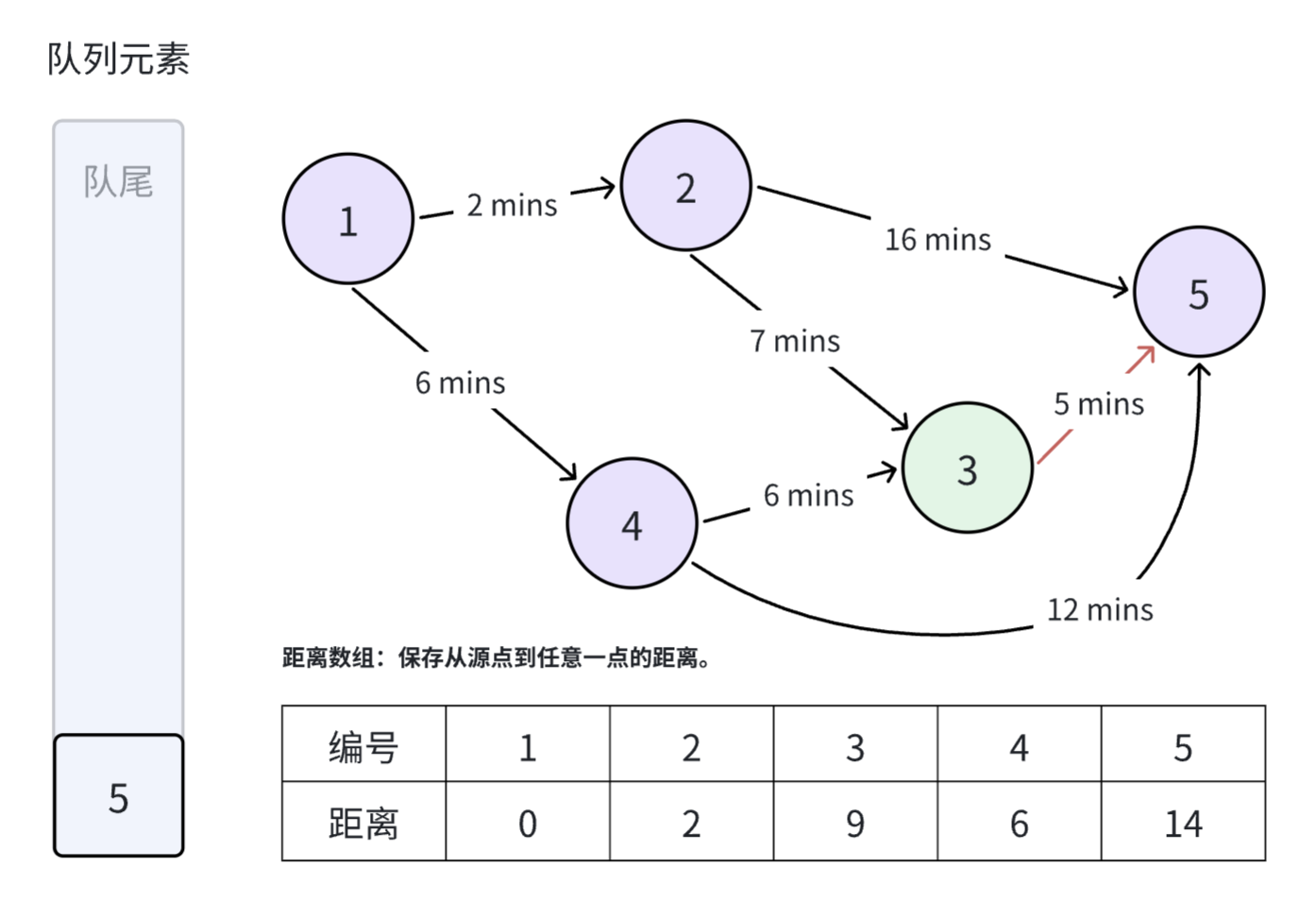
弹出位于队首的 号元素,选择位于队首的 号元素,由于该节点不存在任何的后继节点,因此不做任何操作,直接将 号节点弹出队列。至此,队列为空,SPFA 算法结束。
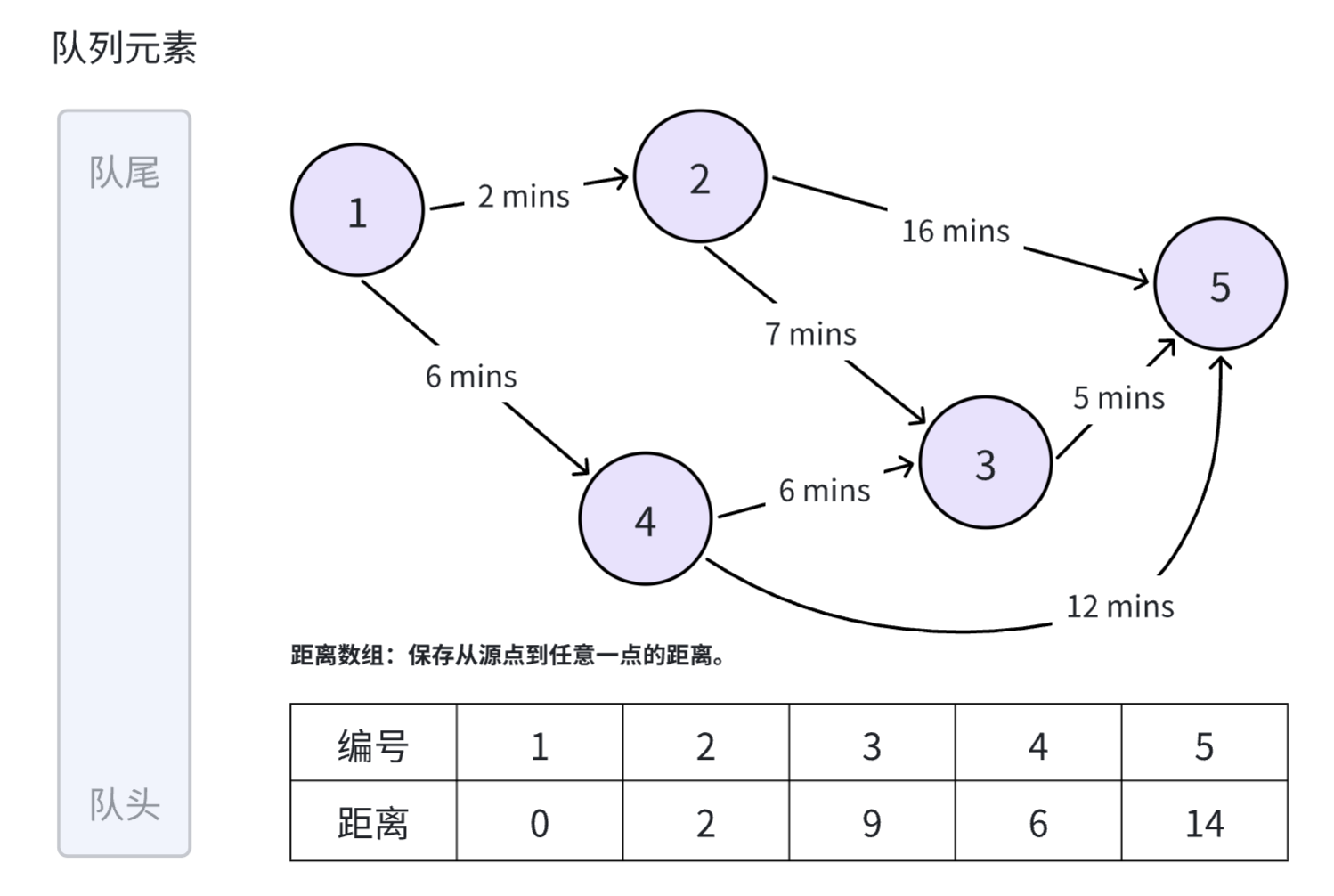
完整的 SPFA 求解最短路的代码如下(对应例题:洛谷 - P4779 【模板】单源最短路径(标准版) 和 ACGO - A569.单源最短路径1,由于标准版的 SPFA 算法最坏的情况会被卡死,因此不保证可以通过所有的测试点):
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#define int long long
using namespace std;
const int N = 1e6;
int n, m, s, dis[N], inque[N];
struct Edge{
int to;
int weight;
}; vector<Edge> G[N];
void SPFA(int origin){
// 初始化:将所有非起点外的点都初始化为正无穷大。
for (int i=1; i<=n; i++)
dis[i] = 2147483647;
dis[origin] = 0;
// 将源点加入到队列之中。
queue<int> que;
que.push(origin);
inque[origin] = 1;
// 循环直至队列不为空。
while(!que.empty()){
int t = que.front();
inque[t] = 0;
que.pop();
for (Edge next : G[t]){
// 进行松弛操作。
if (dis[t] + next.weight < dis[next.to]){
dis[next.to] = dis[t] + next.weight;
// 如果不在队列之中,就将点加入队列。
if (!inque[next.to]){
que.push(next.to);
inque[next.to] = 1;
}
}
}
}
return ;
}
signed main(){
// 输入输出优化。
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
// 读入题目数据并建图。
cin >> n >> m >> s;
for (int i=1, u, v, w; i<=m; i++){
cin >> u >> v >> w;
G[u].push_back((Edge){v, w});
}
// 运行最短路算法。
SPFA(s);
// 输出结果,如果 dis 还是正无穷大,则证明改节点无法到达。
for (int i=1; i<=n; i++)
cout << (dis[i] == 2147483647 ? -1 : dis[i]) << " ";
return 0;
}
使用该算法判断负环,只需要判断是否存在一个节点被加入了超过 次即可。完整的 SPFA 判断是否存在负环的代码如下(对应例题:洛谷 - P3385 【模板】负环):
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#define int long long
using namespace std;
const int N = 1e6;
int T, n, m, s;
int cnt[N], dis[N], inque[N];
struct Edge{
int to;
int weight;
}; vector<Edge> G[N];
void SPFA(int origin){
// 初始化:将所有非起点外的点都初始化为正无穷大。
for (int i=1; i<=n; i++)
dis[i] = 2147483647;
dis[origin] = 0;
// 将源点加入到队列之中。
queue<int> que;
que.push(origin);
inque[origin] = 1;
// 循环直至队列不为空。
while(!que.empty()){
int t = que.front();
cnt[t] += 1;
inque[t] = 0;
que.pop();
if (cnt[t] >= n){
cout << "YES" << endl;
return ;
}
for (Edge next : G[t]){
// 进行松弛操作。
if (dis[t] + next.weight < dis[next.to]){
dis[next.to] = dis[t] + next.weight;
// 如果不在队列之中,就将点加入队列。
if (!inque[next.to]){
que.push(next.to);
inque[next.to] = 1;
}
}
}
}
cout << "NO" << endl;
return ;
}
void solve(){
// 读入题目数据并建图。
cin >> n >> m;
for (int i=1; i<=n; i++){
G[i].clear();
inque[i] = 0;
cnt[i] = 0;
}
for (int i=1, u, v, w; i<=m; i++){
cin >> u >> v >> w;
G[u].push_back((Edge){v, w});
if (w >= 0) G[v].push_back((Edge){u, w});
}
SPFA(1); // 判断是否存在负环。
}
signed main(){
// 输入输出优化。
ios::sync_with_stdio(0);
cin.tie(0); cout.tie(0);
cin >> T; while(T--) solve();
return 0;
}