迪克斯特拉算法

迪克斯特拉算法 Dijkstra Algorithm

Dijkstra 算法是一种用于寻找图中从单一源节点到其他所有节点的最短路径的算法（即单源最短路径算法）。它适用于所有边权重为非负值的图。这个算法最早是被荷兰计算机科学家艾兹赫尔·戴克斯特拉 (Edsger W. Dijkstra) 发明并提出的，因此用他的名字来命名该最短路算法。

Dijkstra 算法的基本思想是逐步扩展最短路径，直到覆盖所有节点。依旧以「场景引入」章节的图来举例子，虽然我们没有办法一下子立刻求解出从 $1$ 号节点到 $5$ 号节点的最短路径，但是如果我们能求出从 $1$ 号节点到 $5$ 号节点所有的前驱节点的最短路径，那么我们就可以立刻计算出从起点到 $5$ 号节点最短路。

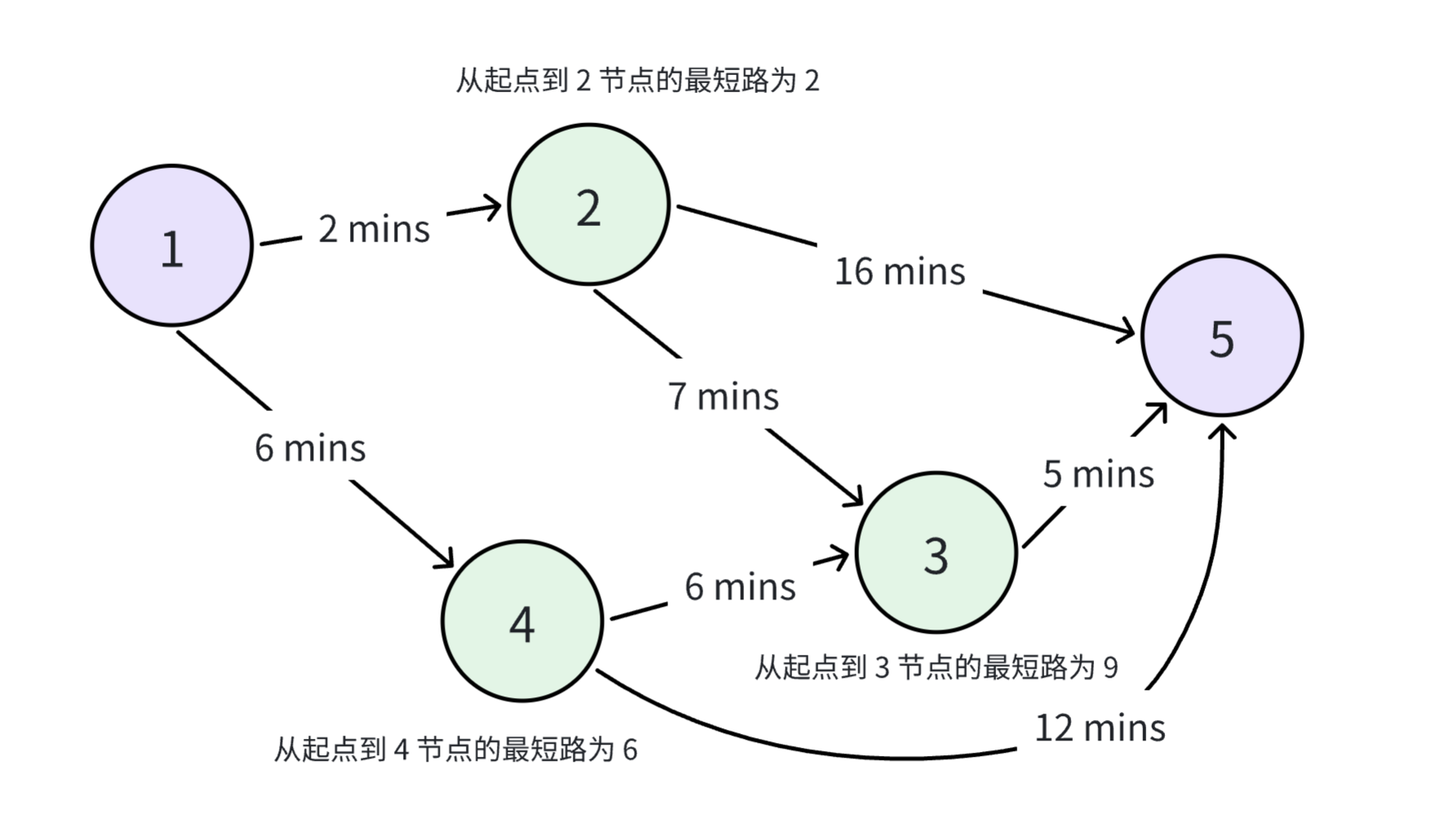
dijkstra-01

如上图所示， $5$ 号节点有三个前驱节点，分别是节点 $V = \{2, 3, 4\}$ ，走到这三个节点的最短距离分别为两分钟、九分钟和六分钟。通过遍历这些前驱节点，我们就可以求出从起点到终点的最短路。显然，对于图中所有的节点，我们都需要按照一定的顺序依次对它们进行相同的操作。这样子，我们就可以求解出从起点开始到图中任意一个点的最短距离了。

Dijkstra 算法具体的实现流程如下：

初始化：

创建一个数组，用于记录从源点开始到任意一点的距离。同时设定源节点的距离为 $0$ ，其他所有节点的距离为 $+\infty$ 。
将所有节点标记为未访问。
使用一个优先队列来存储节点及到某一个节点当前所计算出的最短距离。

选择节点：

从未访问的节点中选择当前距离最小的节点作为当前节点。
PS：如没有特殊情况，一开始这个节点应该是求解最短路问题的起点（起点与自己的距离应该是 $0$ ，正如初始化步骤中所提及的）。

更新节点：

对于当前节点的每个邻居节点，计算从当前节点到该邻居节点的距离。
如果这个距离小于已知的到该邻居节点的距离，则更新该邻居节点的距离。
距离更新: 对于每个邻居节点，计算从起点到该邻居节点的距离，如果该距离小于已知的最短距离，则更新最短距离。

标记已访问：

将当前节点标记为已访问，表示已经处理完了该节点。
PS：当节点被标记完已访问后，从起点到该节点的最短距离就已经被正式确定下来了，在后续的计算过程中该节点的距离将不会再被更新。标记节点已访问可以在「选择节点」步骤完成后时就进行。换句话说，第三步和第四步的顺序并不重要。

重复循环：

重复上述提到的第 2-4 步，直到所有的点都被标记为已访问。

以下是使用 Dijkstra 算法对例题的模拟过程：

首先初始化距离数组，将源点的距离设置为 $0$ ，将除源点以外的所有点的距离设置为 $+\infty$ 。正无穷大表示到达该点的最短距离还未知。

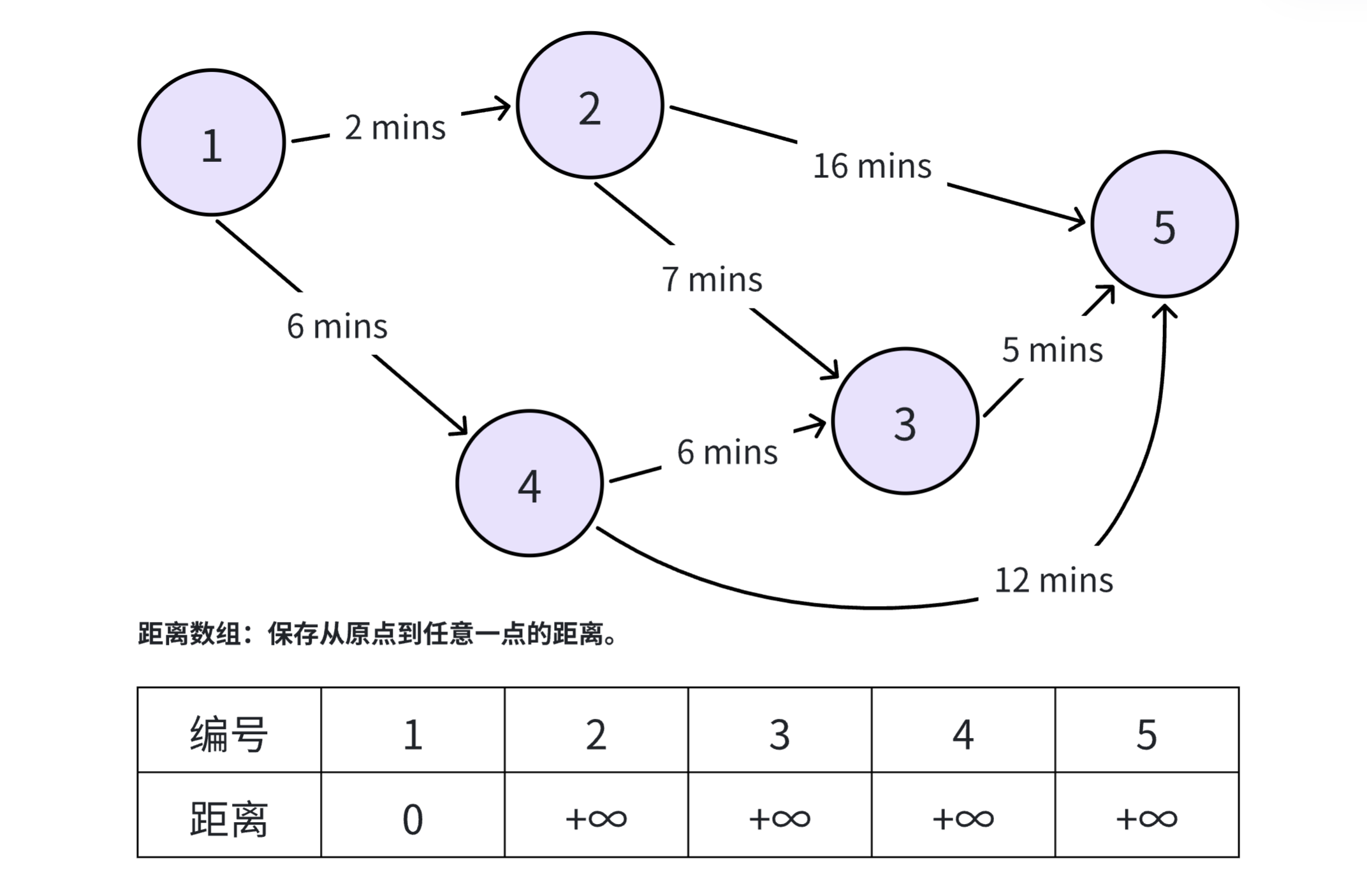
dijkstra-02

从未访问的节点中选择当前距离最小的节点作为当前节点。在一开始，距离最小的节点就是源点本身。如下图，浅绿色表示当前选中的节点，黄色表示该节点的邻居节点。接下来就开始更新两个邻居节点距源点的最近距离。从 $1$ 号点到 $2$ 号点的最短距离为 $2$ ，而 $2$ 号节点当前所记录的最短距离是 $+\infty$ ，比较发现 $2 < +\infty$ ，因此将 $2$ 号点的距离从原本的正无穷更新为 $2$ 。节点 $4$ 也是如此，从起点到该节点的最短路径将由原本的正无穷更新为 $6$ 。

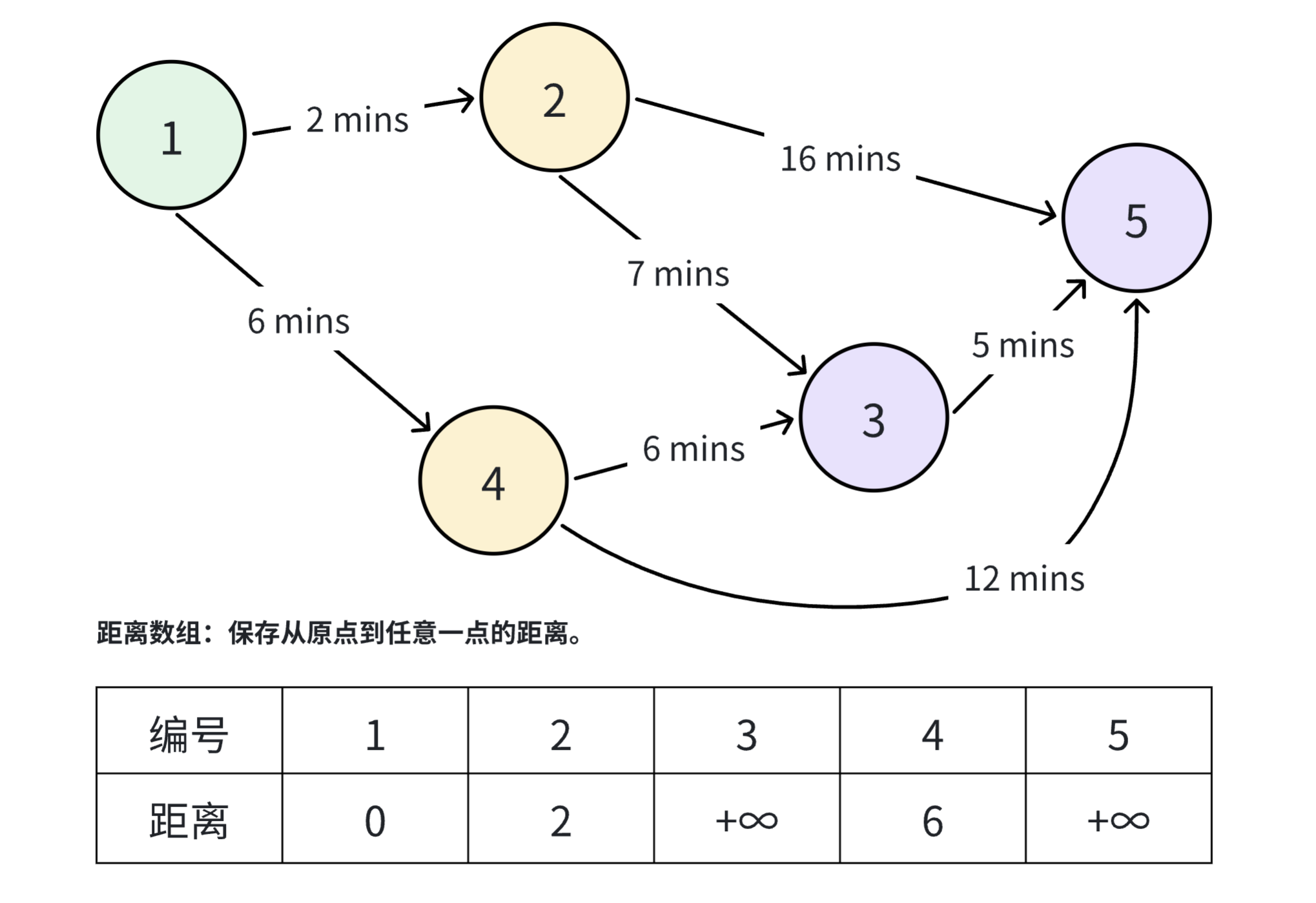
dijkstra-03

此时， $1$ 号节点已经处理完成了，我们将该节点标记为已访问（图中用深绿色表示）。接下来，我们从未访问的节点当中选择一个距离最小的节点作为当前节点。如下图，未访问的节点有 $V = \{2, 3, 4, 5\}$ ，其当前的距离分别为 $Dis = \{2, +\infty, 6, +\infty\}$ ，因此我们选择 $2$ 号节点作为新的当前节点，因为该节点是所有未访问节点当中距离源点距离最小的那个节点。

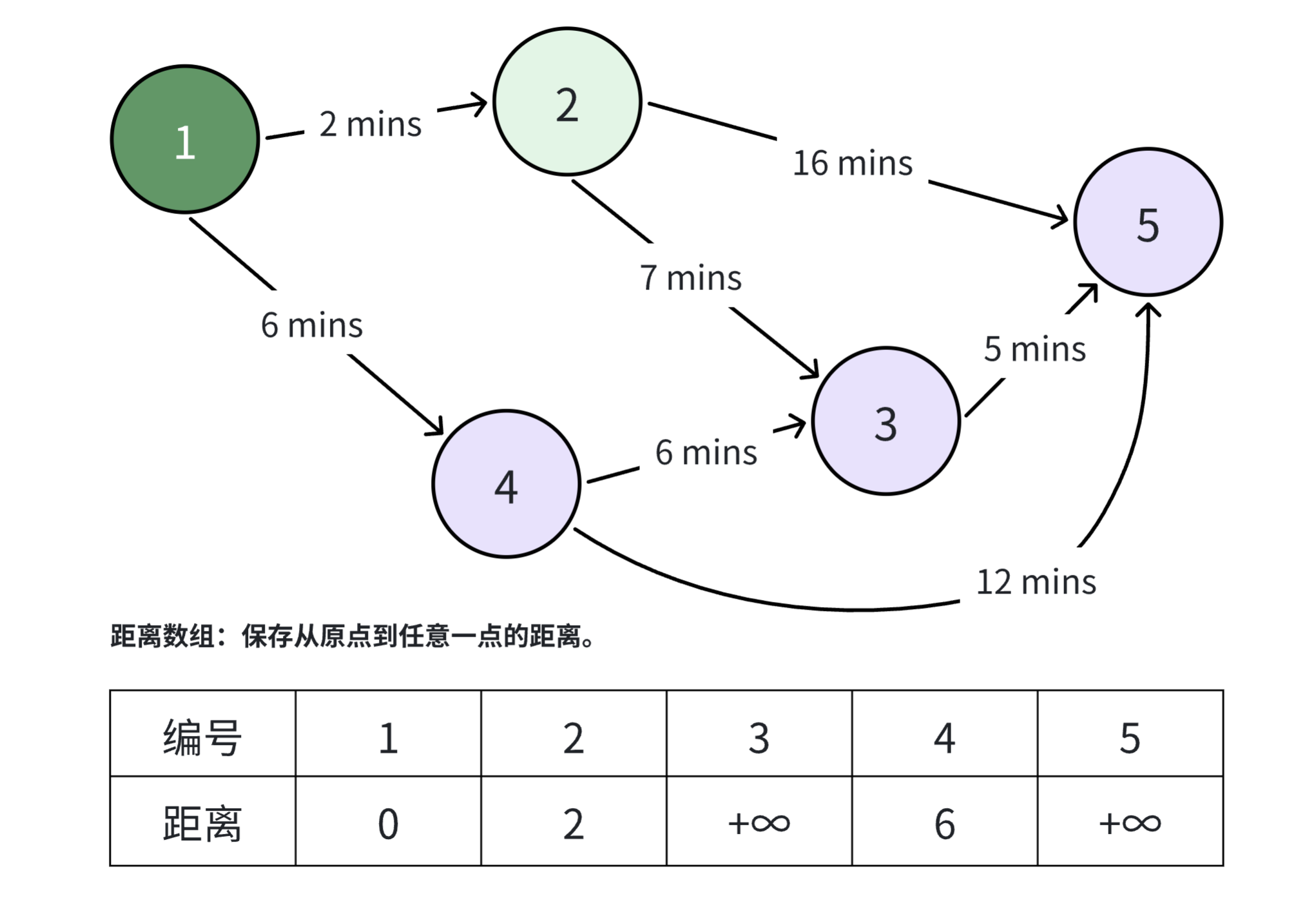
dijkstra-04

从 $2$ 号节点开始，更新该节点的所有邻居节点。对于 $5$ 号节点，原本的距离是 $+\infty$ ，但从源点出发，经过 $2$ 号节点的距离为 $2 + 16 = 18$ ，显然这个距离比原本的正无穷大更优，因此更新该节点的最短距离为 $18$ 。对于 $3$ 号节点也是如此，从源点出发经过 $2$ 号节点的最短距离是 $2 + 7 = 9$ ，因此将 $3$ 号节点的距离更新为 $9$ 。

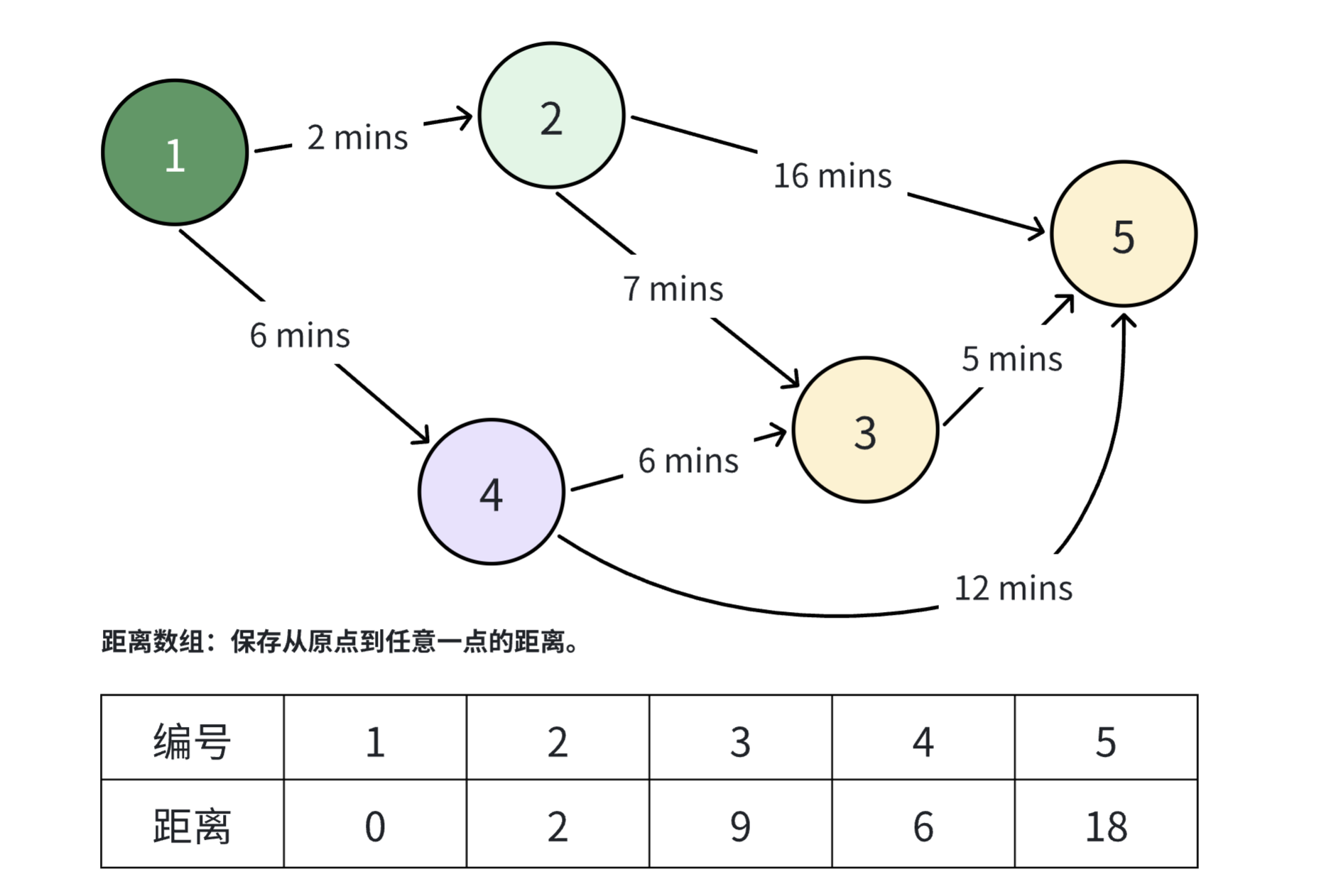
dijkstra-05

将 $2$ 号节点标记为已访问。接下来再从未访问的节点中选择一个距离最近的节点，现在未访问的节点有 $V = \{3, 4, 5\}$ ，其中 $4$ 号节点的距离最短，因此选择 $4$ 号节点作为当前节点。从 $4$ 号节点出发可以到达的节点只有 $3$ 号节点，如果从源点出发经过 $4$ 号节点再到 $3$ 号节点的距离为 $6 + 6 = 12$ ，这显然比当前 $3$ 号的距离更大，因此这不是一个更优的解，本轮将不再更新 $3$ 号节点的最短距离。

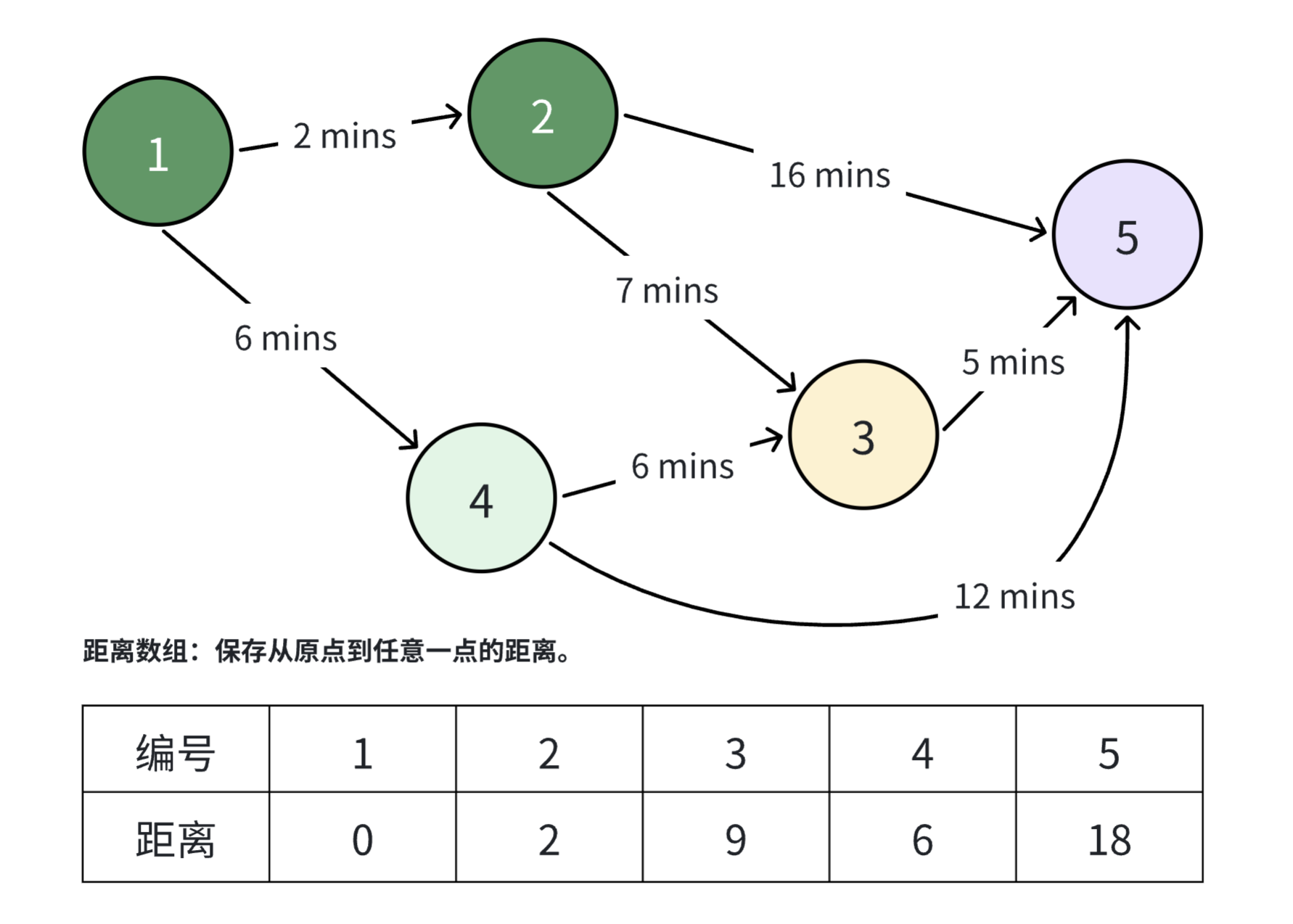
dijkstra-06

将 $4$ 号节点标记为已访问。现在再从未访问的节点中选择一个距离最小的节点作为当前节点，因此我们将选择 $3$ 号节点作为当前节点。我们发现从源点出发经过 $3$ 号节点到 $5$ 号节点的距离为 $9 + 5 = 14$ ，这比 $5$ 号节点当前记录的 $18$ 更优，因此更新 $5$ 号节点的最短距离。

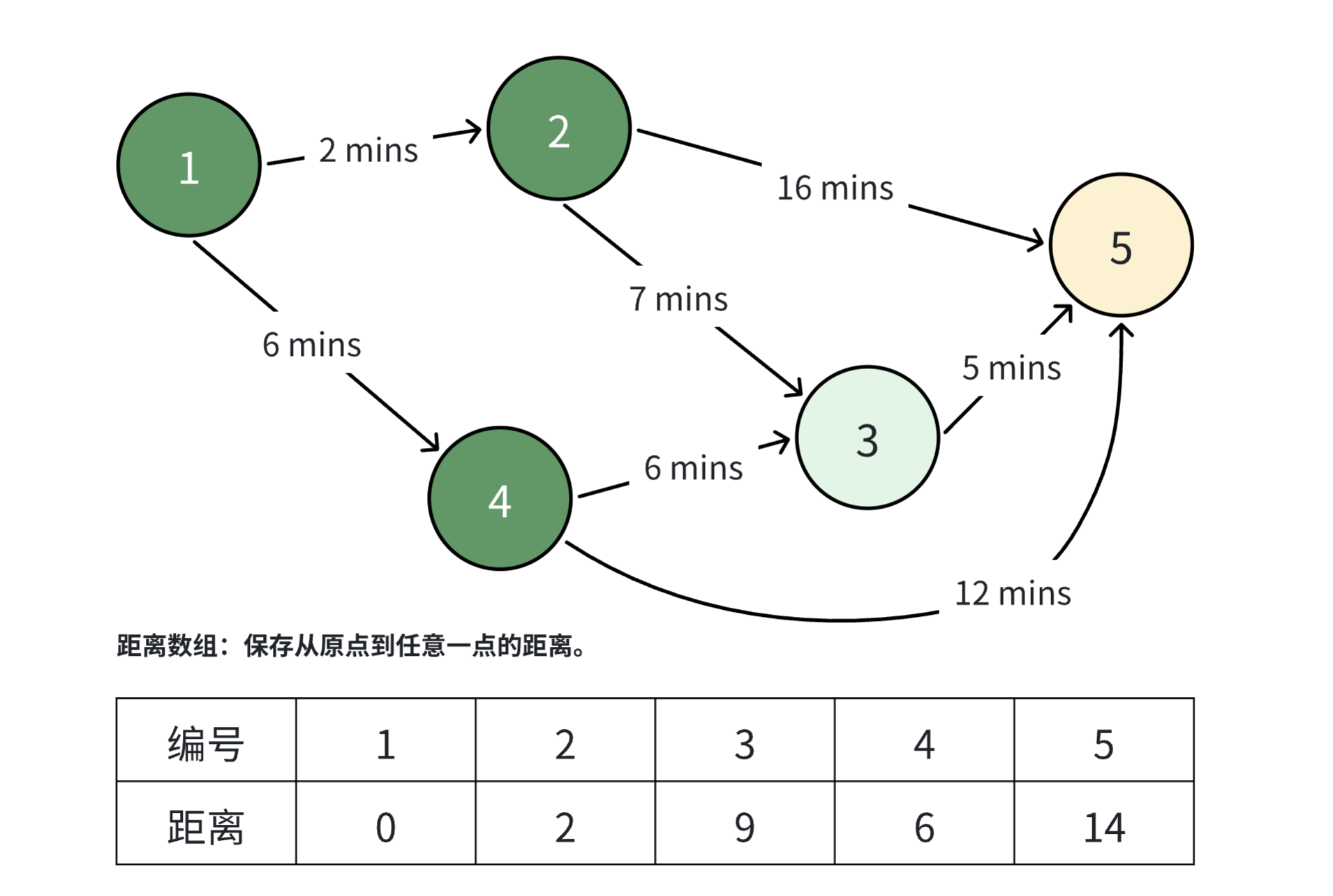
dijkstra-07

将 $3$ 号节点标记为已访问。

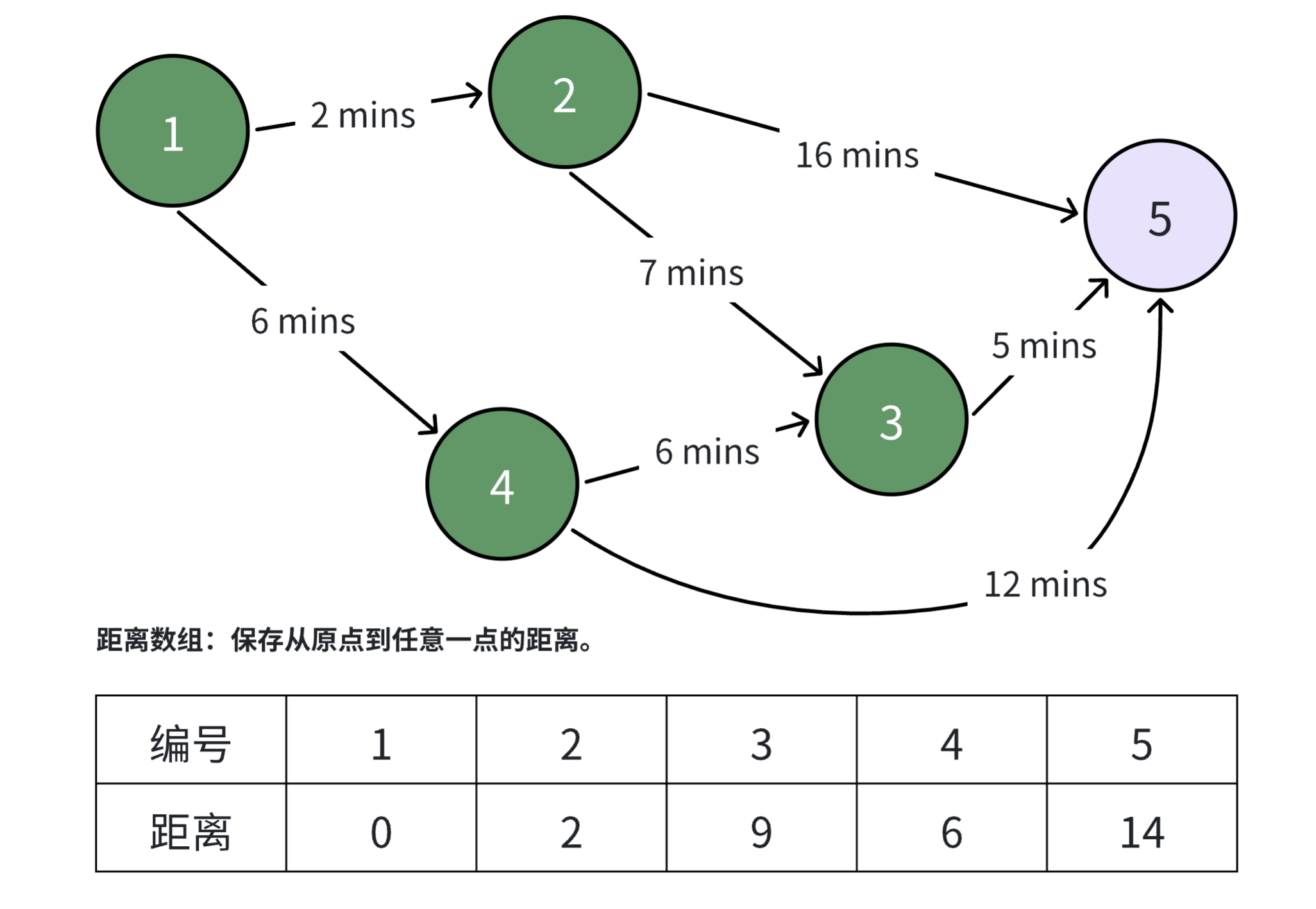
dijkstra-08

选择 $5$ 号节点作为当前节点。由于 $5$ 号节点没有任何的后继节点，因此循环结束。将 $5$ 号节点标记为已访问。

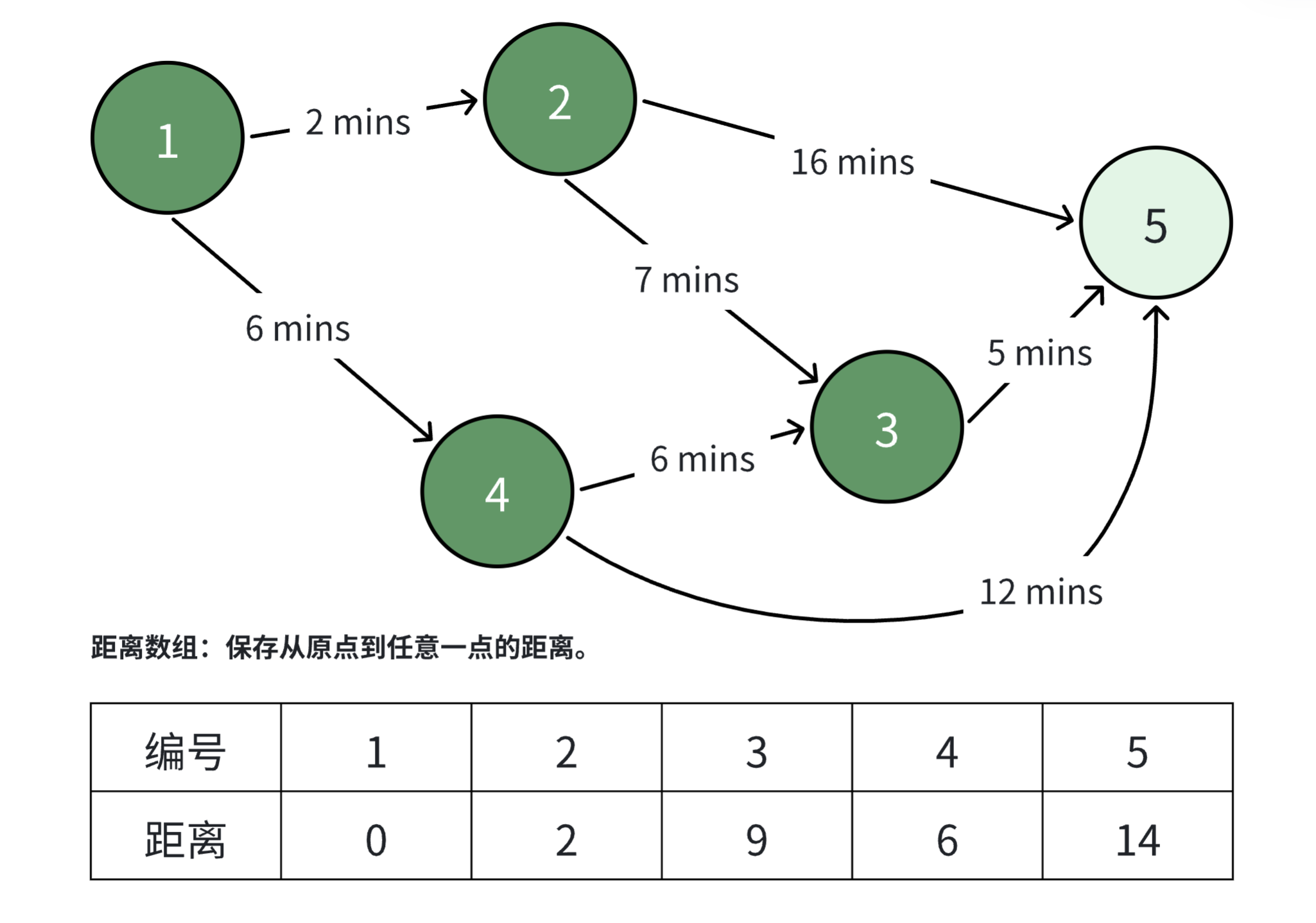
dijkstra-09

至此，所有的节点都标记为已访问，Dijkstra 算法结束。此时距离数组记录的值就是从源点出发到各个点的最短距离。

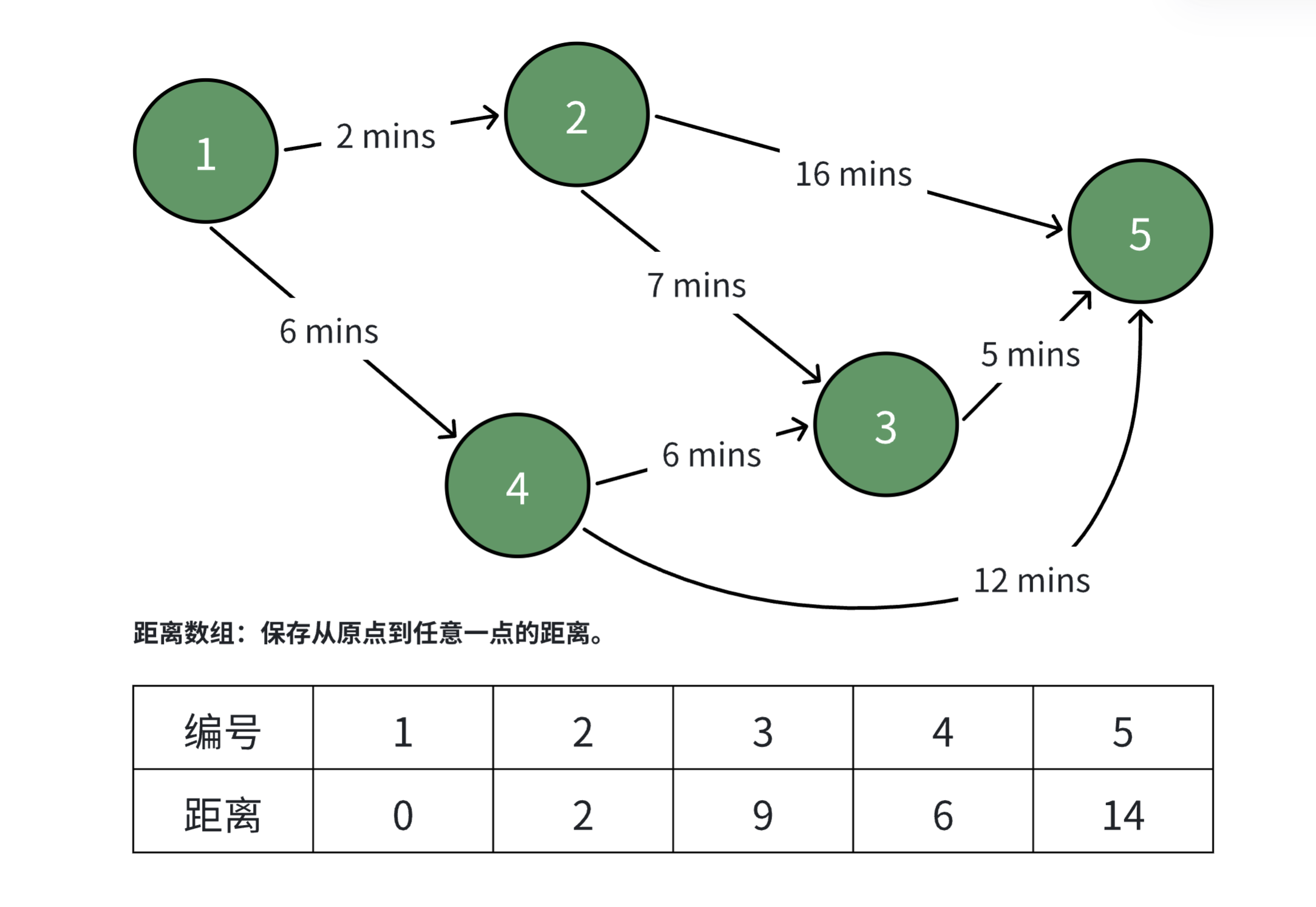
dijkstra-10

在下方代码中，为了快速的找到当前距离最小的节点，我们将会使用 C++ 自带的优先队列 (Priority Queue) 数据结构来实现。

完整的 Dijkstra 求解最短路的代码如下（对应例题：洛谷 - P4779 【模板】单源最短路径（标准版）和 ACGO - A569.单源最短路径1）：

#include <iostream>
#include <algorithm>
#include <queue>
#include <vector>
#define int long long
using namespace std;

const int N = 1e6;

int n, m, s;
int u, v, w;
struct Edge{
    int to;
    int weight;
}; vector<Edge> G[N];
struct node{
    int position;
    int distance;
    // 优先队列优化，按照 distance 从小到大进行排序。
    bool friend operator < (node a, node b){
        return  a.distance > b.distance;
    }
};
// dis 数组用于记录从起点开始到任意一个点的最短路。
// vis 数组用于记录一个节点是否已经被访问过了。
int dis[N], vis[N];

void dijkstra(int origin){
    // 初始化：将所有非起点外的点都初始化为正无穷大。
    for (int i=1; i<=n; i++)
        dis[i] = 2147483647;
    dis[origin] = 0;

    // 优先队列初始化：一开始将起点加入队列。
    priority_queue<node> que;
    que.push((node){origin, 0});

    while(que.size()){
        node t = que.top();
        que.pop();

        // 如果节点被访问过了，则略过。否则标记该节点为已访。
        if (vis[t.position]) continue;
        vis[t.position] = 1;  // 也可以写在最后。

        // 遍历所有的邻居节点。
        for (Edge next : G[t.position]) {
            int to = next.to;
            int w = next.weight;
            // 如果存在一条更优秀的路径，则更新最短路。
            if (dis[to] > w + dis[t.position]){
                dis[to] = w + dis[t.position];
                // 将节点加入到优先队列之中。
                que.push((node){to, w + dis[t.position]});
            }
        }
    }
    return ;
}

signed main(){
    // 输入输出优化。
    ios::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);

    // 读入题目数据并建图。
    cin >> n >> m >> s;
    for (int i=1; i<=m; i++){
        cin >> u >> v >> w;
        G[u].push_back((Edge){v, w});
    }

    // 运行最短路算法。
    dijkstra(s);

    // 输出结果，如果 dis 还是正无穷大，则证明改节点无法到达。
    for (int i=1; i<=n; i++)
        cout << (dis[i] == 2147483647 ? -1 : dis[i]) << " ";
    return 0;
}

由于该算法是基于优先队列实现的，优先队列求出最小值的复杂度为 $O(log_2(V))$ （使用了二叉堆优化），因此 Dijkstra 的时间复杂度约为 $O((V + E) \times log_2{V})$ ，其中 $V$ 代表图中顶点的数量， $E$ 代表图中边的数量。相比之下，Dijkstra 算法的运行效率非常优越。该算法也是在求解最短路问题中应用最广泛的算法之一。

迪克斯特拉算法 Dijkstra Algorithm​

迪克斯特拉算法 Dijkstra Algorithm